視覚化にハマり、いろんなものを描いてます。
反比例、比例に続き、今回は1次関数です。
1次関数は比例を発展させたものです。
比例が「原点を通る直線」なら、1次関数は「原点を通らない直線」です。
本当は1次関数の中に比例が入ってます。
”直線”が「1次関数」。
その中で、たまたま”原点を通った直線”を「比例」と呼んでいるだけです。
長方形の中に正方形が入っているのと同じパターンです。
長方形の性質を持ちつつ、たまたま”縦と横の線分の長さが同じになった”のが正方形です。
さて話を戻して1次関数ですが、これを一般的なテキストはどう扱っているかというとこうです。
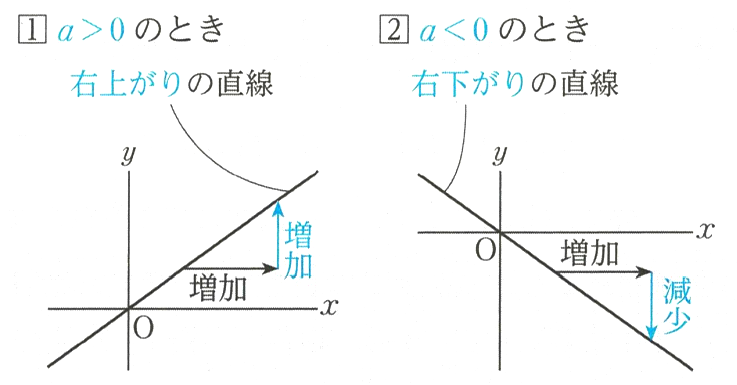
可もなく不可もなしですね。
私が真面目に描いたら、同じように描くでしょう。
 SHIMIZU
SHIMIZUだってこうとしか説明しようがないんだもの
そこで「印象に残す」一点で描いたものを紹介します。
1次関数は比例とセットで覚えましょう。
なので、以前の比例をまず出します。
比例はこちらでしたね。


そして、今回の一次関数はこちら!!
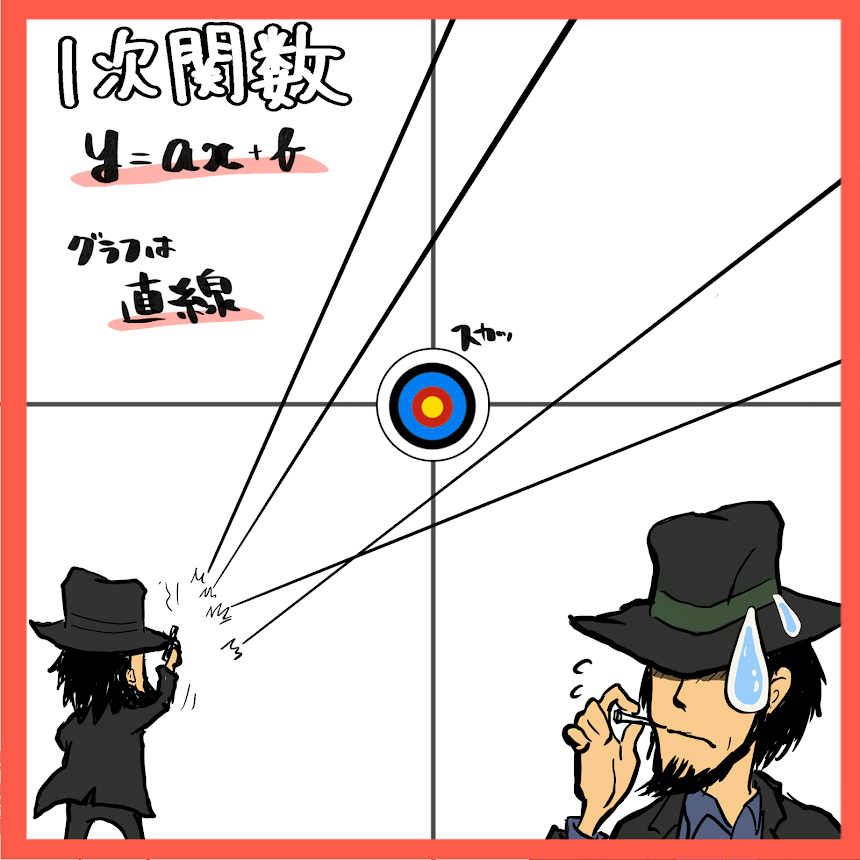

一言で言うなら「銃を撃つのが下手な次元」ですね。



次元って今の子にも通じるの?



通じると信じたい
原点を通らない直線、つまり中心を撃ち抜けない弾丸です。
原点を通らない直線はすべて「1次関数」です。
たまたま中心を撃ち抜いてしまったら、つまり原点を通ってしまったら、それは「比例」と呼びましょう。
1次関数ではあるのですが、比例という名前がついているので、そういう場合は名前を呼んであげましょう。
正方形を長方形って呼んでも間違いとは言いませんが、「あれは正方形だよ」と言いたくなるでしょう?
長方形の一種であっても、特別に名前がついている正方形は、やっぱり正方形と呼んであげるのが良いのです。
比例も、1次関数の一種であっても、比例と呼んであげましょう。
ということで、原点を通った直線は比例、原点を通らなかった直線は1次関数です。
原点を通らなかったせいで、1次関数には「+b」がついてますね。
y=ax が比例
y=ax+b が1次関数
比例は「原点を通る直線」
1次関数は「直線」
です。
以上、印象に残す1次関数でした。