今日は日曜日。
朝から開校しています。
午前中は3年生に混じって2年生の姿もありました。
2年生の4割が今日の午前中に来ました。
 SHIMIZU
SHIMIZU定期テストが近いからかな



部活ってないの?



日曜日はないみたいね



ずいぶん楽になったもんだ
それにしても2年生達、お昼はまたぐわ、最後までやっていくわ、なんかすごいんですけど。
3年生より長い時間勉強してました。



将来有望だ
話は変わって、問題です。
∠xは何度でしょうか?
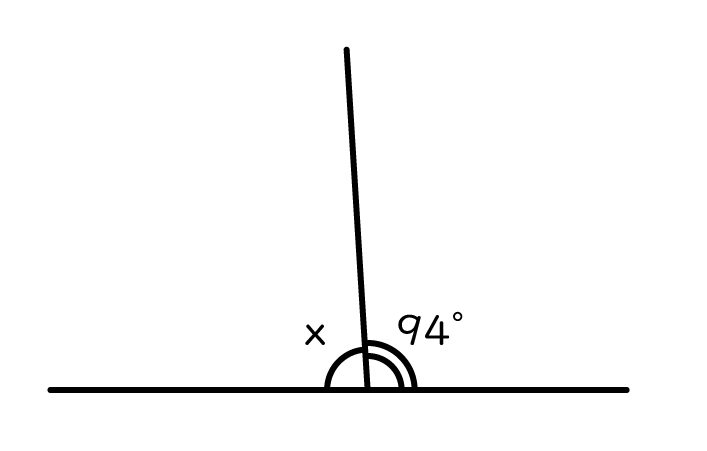




86°



正解
もちろん答えは86°です。
一直線の180°から94°を引けば簡単に求められますね。
それは中学生も皆分かっています。
よって、皆、180-94=86 とするのです。



まあ、そうだろうね
そして、この計算をするときに筆算をするのです。



まあ、するだろうね
でも、この時もっと簡単な計算があります。



計算というか考え方かな



足し算で考えるってやつ?



それも一つ
引き算を足し算にするのは以前にも記事にしましたね。
180-94=86 ではなく
180=94+86 で考えるというものです。
ただ、これも今回はちょっと難しいです。



繰り上がりがあるしね
では、どうするかというと……
90-4=86 です。
なんで?
もし、線が垂直になっているのであれば、左の角と右の角はどちらも90°ですよね。
でも、今回は線が垂直ではありません。
ちょっと左に傾いています。
右の角がちょっと左に侵略しています。
具体的には、右の角は左に4°侵略しているので、90+4=94 になっているわけです。
逆に言えば、左の角は4°侵略されているので、90-4=86 となるわけです。
こんな風に「垂直の線だったら、90°と90°で分けられる」ということが頭に入っていれば、そこから少し左右にずらせば良いだけのことです。
これなら180°から引かなくても、90°から引けば良いだけ。
3桁からの引き算より、2桁からの引き算の方が簡単ですよね。
こんなふうな工夫をすると、計算を速く正確にできます。
毎回筆算するよりも「もっと簡単に求められる工夫はないか」と考える心を持っていきましょう。