頭の中は覗けないものですが、推測はできます。
数学の途中式や計算式、筆算を見ればわかります。
三角形があります。
それぞれの角を∠A, ∠B, ∠Cとします。
∠A=71°, ∠B=23°である場合、∠Cの外角は何度でしょう?
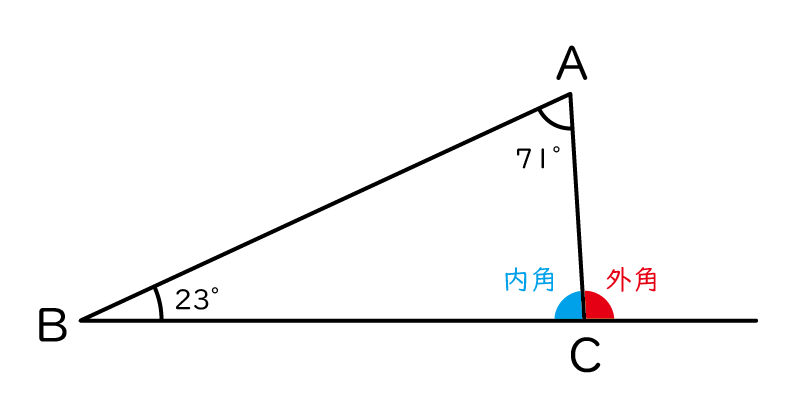
こういった問題のときに、∠Cの内角を求めてから、それを使って外角を求める子がそこそこいます。
 友人Y
友人Y合ってるでしょ?別にいいんじゃないの?



合ってるけど、遅いし間違える確率が上がっちゃうの
∠Cの内角は、三角形の内角の和である180°から∠Aと∠Bの和を引いて求めます。
180 – ( ∠A + ∠B )
= 180 – ( 71 + 23 )
= 180 – 94
= 86
ということで、内角の∠ACBは86°です。
そして、直線の180°から内角を引けば、外角が求められます。
180 – 86
= 94
94°で合っているのですが、計算している途中で「何を求めているのかわからくなる」という可能性があります。
最初に86°と答えが出た時点で、それを解答用紙に書いてバツをくらってしまうことがよくあります。
そして、足し算や引き算を何回かやるので、その間に計算間違いをする可能性もあります。
なので、おすすめは「∠A+∠B=∠Cの外角」です。
これを言葉でいうと「三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい」となります。
でも、面倒なので「スリッパ型」と一言で片付けてしまいます。
平行線を引いて証明する方法もありますが、今回は計算式で証明してみましょう。
まず、∠ACB(∠Cの内角)の求め方は 180 – ( ∠A + ∠B ) でしたね。
そうやって内角を求めたら、今度は 180 – 内角 をして外角を出すわけです。
ということは
180 – { 180 – ( ∠A + ∠B ) }となります。
中括弧{ } を外すと
180 – 180 + ( ∠A + ∠B )
となり、180と-180で0になってしまうので、残るのは
∠A + ∠B
だけとなります。
よって∠Cの外角は、∠A+∠Bで求められます。
今回の数字を使うなら、71+23 で、84°と答えを出せます。
これなら足し算一回ですので、計算ミスをする可能性も極力低くなったでしょう。
足し算と引き算では、引き算の方が難しいと感じるのが一般的かと思います。
でも、引き算と足し算は似たようなものです。
例えば98-46なら答えは52ですね。
98-46=52
でもこれを
98=46+52
と変えることができます。
98ー46を
98=46+▢
にします。
これでも「52」と答えられますね。
頭の中を除いてみると、こうやって簡単に計算しやすい方法をしていませんか?
私は結構、足し算で考えていることが多いです。
100-46と言われたら、とっさに「46に何を足したら100になるか」を考えて、54と答えているのです。
頭の中のそろばんを弾いて54とも出せますが、そろばんは2桁×2桁のときに使うくらいで、100-46くらいなら足し算で考えてしまいます。
236円のもの買うときに1000円を出したらお釣りはいくら?というときも、236に何を足せば1000円になるかをとっさに考えます。
その時は繰り上がりも考えるので「はっぴゃく…」ではなく「ななひゃく」から考えます。
十の位も同様に「ななじゅう…」ではなく「ろくじゅう」です。
一の位は10になるようにするため「4」です。
ということで、764円のお釣り。
でも、こういう方法もあると聞いて驚いたのを覚えています。
それは999円から236円を引いて、最後に1円を足すというものです。
1000円から236円を引くと、繰り下がりがあるので間違えやすいのですが、999円からだとそれがなくなります。
999-236=763
そこに最初に引いておいた1円を足して、764円。



よくそんなこと思いつく人がいるもんだね
いずれにせよ、計算を速く正確にやるための策です。
こういったものが他にもあるので、このブログにて紹介していこうと思います。